안녕하세요!
오늘은 머신러닝의 기본이 되는 probability와 Bayesian Learning에 대해 알아보려 합니다.
'확률과 불규칙 신호'과목에서 배운 내용인데 일단 다 까먹었고 ㅎㅎ...
하지만 중요한 내용이기 때문에 짚고 넘어가 보겠습니다!
< Probability & Bayesian Rule >
- Probability & Statistics 사용 이유

위 사진은 헤드셋 낀 사람의 옆모습을 'DOG'라 인지한 사진입니다. (진짜 강아지 같긴 합니다)
이렇게 컴퓨터가 잘못된 판단을 내리지 않게 delicate한(정교한) 작업을 진행해야 합니다.
real world의 data들은 uncertain하고 ambigous하기 때문에 >확률적인 개념<을 이용하여 제대로된 결과를 내야합니다.
확률을 이용했을 때, 위 사진에서 DOG일 확률을 P(DOG)=0.6, 사람일 확률이 P(PERSION)=0.4와 같이 확률로 나타냄으로써, 여지를 남길 수 있습니다.
추가적인 process를 거치고 위 확률이 변하면서 남겨둔 여지를 통해 data를 다시 처리할 수 있게 해야합니다.
이러한 과정을 거치기 위해 '확률'이 Machine learning에서 적용되야 하는 것 입니다!
- Random Variable (RV)
random variable X는 함수로써, 확률 공간 (S, P)를 실제 R로 이어주는 역할을 합니다.
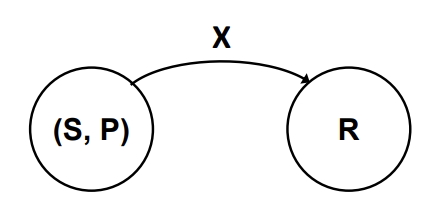
RV X는 discrete한 상황과 continuous한 상황으로 나눠 볼 수 있습니다.
① Discrete Random Variable

위와 같이 discrete한 상황에서는 확률을 p(X = x)로 표현할 수 있습니다. (x ∈ X)
이때 p()를 PMF(Probablity mass function)이라 하고 확률 정보를 제공합니다.
② Continuous Random Variable
반면, Continuous한 상황에서는 특정 값에서의 확률은 구할 수 없고, 구간적인 확률만 구할 수 있습니다.
probabliity a ≤ x ≤ b 를 구하는 과정은 다음과 같습니다.

위 과정에서 보았듯이, p(a ≤ x ≤ b) = F(b) - F(a)로 구해지고, 이때의 F()는 CDF(Cumulative Distribution Function)이라 합니다.
또한 이를 미분하여 나타낸 f()값은 pdf(probability density function)이라 합니다. f(x)>0, ∫f(x) = 1이 항상 만족합니다.
Contnuous한 상황인 Gaussian(Normal) Distribution은 다음과 같습니다.

위 식은 pdf로 나타낸 것 입니다. μ는 E[x]인 평군을 말하고, σ^2는 var[x]로 표준편차를 나타냅니다.
이 식의 CDF값, 적분식은 아래와 같습니다.

- Probalitiy & Bayes Rule
- Joint Probability
확률에서 둘의 연관으로 동시에 일어날 확률은 Joint 확률로 구합니다.
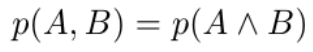
A사건과 B사건이 동시에 일어날 확률은 위와 같이 표현됩니다.
- Conditional Probability
확률에서 B사건이 일어났을 때, A사건이 일어날 확률은 다음과 같은 식으로 표현하고, 이를 조건부 확률이라 합니다.
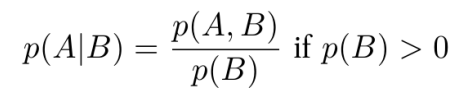
예를들어,
대학교 10000명의 사람은 남자 8000명, 여자 2000명으로 구성되고,
남자 중 피어싱을 한 사람이 100명, 여자 중 피어싱을 한 사람이 900이라 하면
다음과 같은 식과 그림이 도출될 수 있습니다.

- Bayes Rule
조건부 확률을 변형시켜 알고있는 정보들로 식을 구성하는 것이 바로 bayes rule입니다.
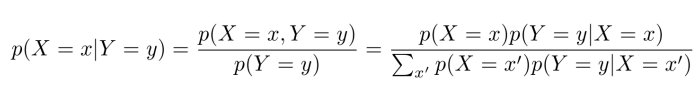
bayes rule은 알고있는 정보가 어떤 것인지에 따라 식을 이용하는 방법이 달라집니다.
- Examples
Ⅰ) Medical Diagnosis Example

다음과 같은 상황을 가정해봅시다.
음성을 T=0, 양성을 T=1, 암이 걸리지 않았을 때를 C=0, 암에 걸렸을 때를 C=1이라 가정하면.
첫번째 줄에 주어진 상황은 P(T=1/C=1) = 0.8임을 말하고, 구해야 하는 것은 P(C=1/T=1)이 됩니다.
표를 통해 주어진 상황을 정리해 보자면,

과 같고, 구하려는 P(C=1/T=1)=720/8720로 매우 낮은 확률이 됨을 확인할 수 있습니다.
즉, 이 cancer 테스트기는 cancer이든 no cancer이든 무조건 0.8의 확률로 random하게 출력하는 잘못된 것임으로 판단할 수 있습니다.
Ⅱ) Credit Example
다양한 상황에서,

일 때의 확률을 고려해 보는 예제입니다.
앞부분인 ⓐShould you work hard to get A+ → P(WH/A+) 으로 표현할 수 있고,
뒷부분인 ⓑIf you work hard, can you get A+ → P(A+/WH) 로 표현할 수 있습니다.
1)

이 상황에서 ⓐP(WH/A+) = 18/20 이고, ⓑP(A+/WH) = 18/20 으로 두 확률이 같게 됩니다.
공부를 열심히 해야되는지 잘 모르겠는 상황이죠.
여기서 "If you work hard, can you get A+?"라 묻는다면,
이 확률은 18/20이므로 "Yes, You have to work hard"라 답할 수 있습니다.
2)

반면 이 상황에서 ⓐP(WH/A+) = 8/20 이고, ⓑP(A+/WH) = 8/10 이 됩니다.
열심히 공부를 안해도 A+이 잘 나오는 것 처럼 보입니다.
3)

마지막으로 위 상황에서는 ⓐP(WH/A+) = 10/12 이고, ⓑP(A+/WH) = 10/20 입니다.
즉, 열심히 공부를 해야지 A+이 나오는구나를 확인할 수 있습니다.
Ⅲ) Ocean View Room Example


이 예제는 "내가 간 곳이 오션뷰일 때, 어떤 호텔을 뽑을 확률이 큰가?"에 대한 질문에 답을하는 예제입니다.
즉, P(A/OC) & P(B/OC) & P(C/OC)를 비교하여 가장 큰 확률인 호텔을 제시해야 합니다.
이 과정을 정석적으로 풀어보면, Hotel A의 경우
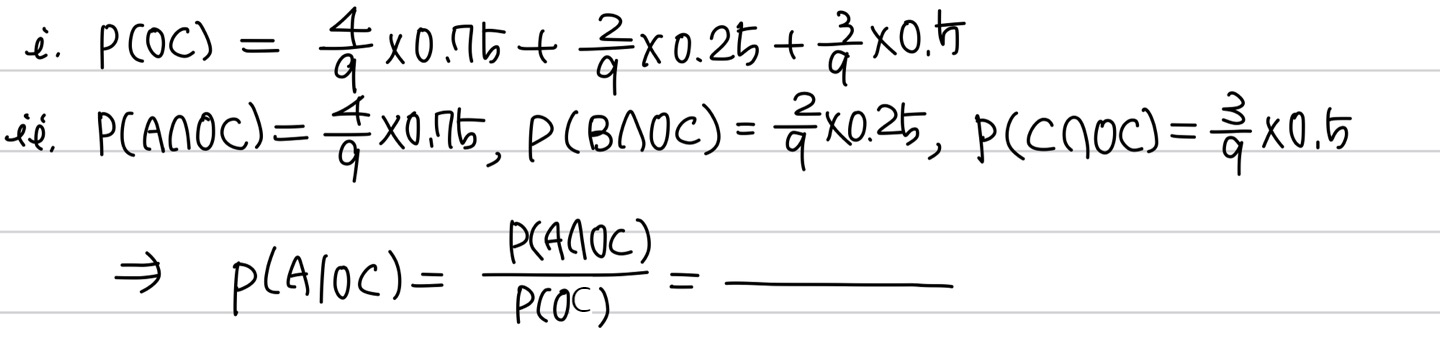
와 같은 과정을 거쳐야 하고, 같은 방법을 진행하면
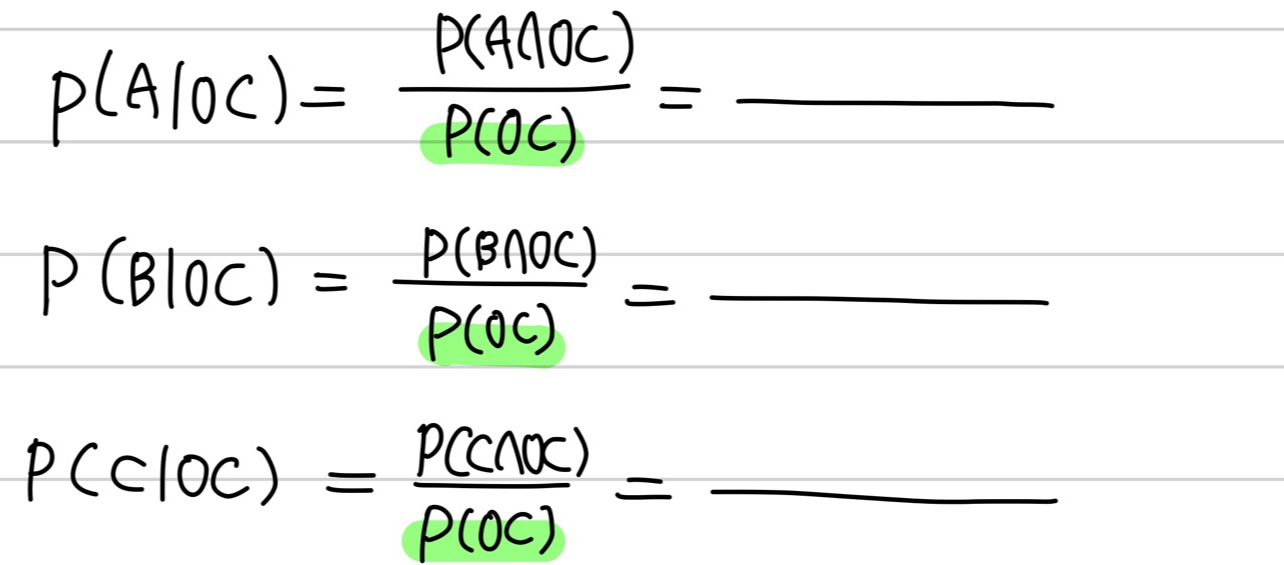
와 같은 수식을 써야하는데, 분모인 P(OC)가 동일하게 유도됩니다.
분모가 같은데 굳이 계산을 통해 이를 진행할 필요가 있을까요?
분자의 비율로 확률의 비중을 구하는 것이 더욱 효율적이고 쉬워보입니다.
그래서 나온 것이 바로 아래입니다.

사후확률인 posterior는 x의 조건을 가지고 발생하고, 이 확률은 주어진 input을 분모로 하고 알고 있는 조건을 분자로 가집니다.
즉, 이미 알고 있는 조건인 분자에 초점을 맞추어

이 확률이 가장 커지는 것을, MAP (maximum a posterior)라고 하는 것 입니다.
결론적으로 이 예제는 분모가 가장 큰 Hotel A일 확률이 가장 높다고 할 수 있습니다.
< Classificaion >
- Applicaion to Classification
Classification에서 가장 많이 쓰이는 예시인 Iris flower 예시를 확인해봅시다.
일단, 모든 머신러닝 과정은 training과정과 prediction과정을 거칩니다.
training은 가지고 있는 data set들을 통해 decision model을 update하는 과정이고,
prediction은 already trained 상태에서 새로운 input을 통해 원하는 ouput을 내는 과정입니다.
Class y ∈ {setosa, versicolor, virginica}, x is 4D feature 상황에서

넣은 꽃은 versicolor의 종임을 다음과 같은 방식을 통해 도출됩니다.
이러한 model은

위와 같은 과정을 거치고, model의 확률 정보는 format과 parameter로 구성되어 있습니다.
- Bayesian Learning
위 상황에 MAP를 적용시켜 보면,

가 되고, paramter인 θ를 고려하여 나타내면

과 같습니다.
Posterior는 주어진 input data에서 가장 큰 확률을 찾아 선택하는 과정임을 알아두어야 합니다!
각 Likelihood와 Prior에 대한 설명은 아래에서 예시를 보며 설명하겠습니다.
< Number Game Example >
- Number Game
일단, number game은 'Likelihood'와 'Prior'가 무엇인가에 대한 이해를 돕기 위해 억지스럽게 만든 게임입니다.
게임 진행 방식은
ⅰ. simple arithmetical concept C를 선택하고, 그때를 나타내를 수들을 D = {x1 , . . . , xN } 로 정의합니다.
ⅱ. 위 concept에 맞는 숫자들 중 하나를 말하고, 다른 수를 맞춰보게 할 때, 그것이 정답일 확률 x' (x^~)을 찾습니다.
주어진 수는 1~100 사이의 수입니다.
만약, "16"을 말했을 때, 어떤 수를 말해야 맞출 수 있을까요?
- 17? 6? 32?
- 99?
위 두 상황 중, 99보다 17, 6, 32가 더욱 likely해보입니다.
즉,
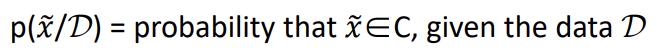
이 확률은 주어진 data set D에서 x' ∈ C일 확률이 되고, Posterior predictive distribution이라 합니다.
위처럼 "16"을 말했을 때 정답에 가까울 것 같은 확률을 나타내면 아래와 같습니다.

이 상황에서 "8", "2", "64" 가 제시된다면, ( D={2,8,16,64} )

와 같이 제시되고, 2의 제곱수 (Power of 2)로 추정할 수 있습니다.
만약 "23", "19", "20"이 제시된다면, ( D={16,23,19,20} )

당연히 이 분포도 달라지게 될것입니다.
자, 그럼 machine에 어떤 기능을 넣어야 할지 우리의 과정을 되짚어 봅시다.
① 가능한 집단 hypothesis space인 H를 넣어줍니다 ( H = 짝수, 홀수, 2의 배수 )
② D = {16} 을 보고 많은 consistent rule을 생각해 봅니다.
③ D = {16, 8, 2, 64}를 보고 "Power of 2"라 생각합니다.
마지막 과정에서 "H = 짝수" 또는 "H = 32를 제외한 2의 배수" 는 왜 생각하지 않을까요?
- Quantifying Likelihood
위 과정을 Likelihood 라고 합니다.
suspicious coincidences, 우연의 일치를 피해 이를 formalize하는 것이 바로 이 과정입니다.
각 원소의 sampling 확률을 같게하여,
model은 D에 따라 가장 간단한 원인일 것이라 판단하는 것을 Occam's razor라고 합니다.
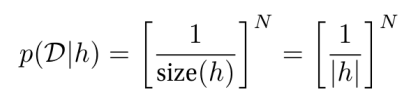
이 Occam's razor를 통해 D = {16}일 때와 D = {16, 8, 2, 64}를 각각 구해보려 합니다.
ⅰ) D = {16}

ⅱ) D = {16, 8, 2, 64}

각각을 통해 suspicious concidence의 정도를 수치화 시킬 수 있습니다.
- Prior
likelihood를 진행하면, h’ = “powers of 2 except 32” 가 h_two = “powers of 2”일 확률이 더욱 큼을 확인할 수 있습니다.
하지만, h’ = “powers of 2 except 32” 인 확률은 너무 억지스러운, conceptually unnatural한 상황이고 이러한 상황을 overfitting이라 합니다.
너무 제시된 data set에 맞추려 하다 보니 과하게 fit되는 상황을 overfitting이라 합니다.
따라서 P(h)라는 값으로 background knowledge를 수치화해 넣어줌으로써, 사람의 주관을 넣어주어야 합니다!
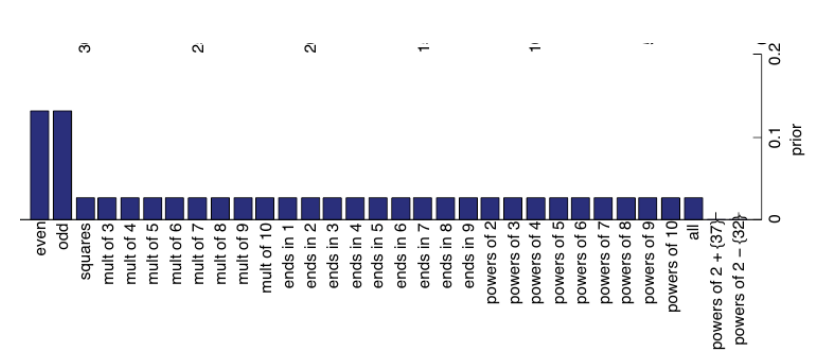
이 게임에서는 위와 같은 prior를 넣어주어 "32를 제외한 2의 배수"와 같은 상황을 미리 제거하는 것 입니다!
training set에 이와 같은 prior을 넣어주어 사람의 사전 지식을 인가해줍니다.
이 prior를 적용하여

다시 D = {16}일 때와 D = {16, 8, 2, 64}를 확인해 봅시다.
ⅰ) D = {16}
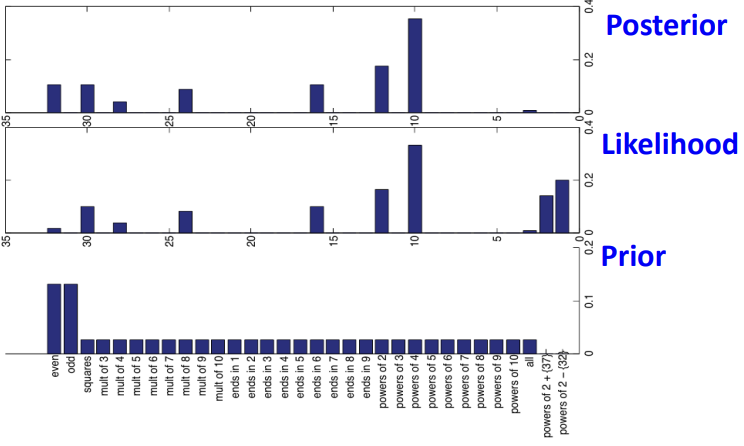
ⅱ) D = {16, 8, 2, 64}
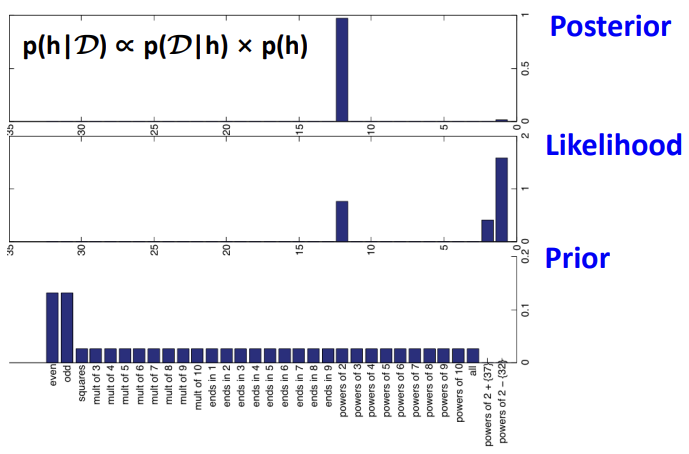
이를 통해 "powers of 2"를 따라 D를 생성하였다고 판단할 수 있게 됩니다!
- MAP estimate & MLE
MAP는 prior가 있고 MLE는 data만 있는, prior가 없는 상황으로 정의합니다.
앞에서 정의한 MAP를 다시 정의해 봅시다.


위 식에서 N이 증가하면 p(h)보다 p(D/h)가 더욱 dominant하기 때문에 MLE에선 overfitting이 될 수 있습니다.
그렇기에 이러한 판단을 방지하기 위해 N을 많이 사용하여 overfitting을 방지할 수 있습니다.
결론적으로,

의 식에서 p(h/D)는 MAP, p(D/h)는 MLE로 작용하고, p(h)는 prior가 됩니다.
p(h)가 constant가 되면 MAP와 MLE는 같아지게 되고,
N이 많을수록 p(h)가 더욱 커지면서 overfitting을 방지할 수 있게 됩니다.
오늘은 여기까지 입니다~
다음글 부터는 본격적인 ML에 대해 배워보겠습니닷!
이번 강의는 아래 링크를 참고해 주세요!
감사합니다 :)

'[학부 일기] 전자공학과 전공 > 머신러닝' 카테고리의 다른 글
| (( 조금은 느린 업데이트 )) (0) | 2023.08.30 |
|---|---|
| [머신러닝] 1. Introduction ML (0) | 2023.06.19 |