안녕하세요!
이번에는 데이터 분석에서 사용하는 '공정능력'에 대해 알아보려 합니다!
( 식스시그마 자격증을 딸 때, 이 내용을 배웠었는데 ... 새록새록하네요 😎 )
- 공정능력
먼저, 공정능력은 '생산공정이 요구조건에 맞춰 얼마나 균일한 품질의 제품을 생산할 수 있는가'에 대한 생산능력치를 말합니다.
품질 관리를 통해 공정의 미래 수행능력을 평가하는 지표가 되는 것이죠.
그리고 규격한계(Spec Limit) 대피 공정의 수행능력을 수치로 표현한 것을 공정능력지수라고 합니다.
중심이 target에 가깝고, 산포가 적어야지 우수하다고 판단합니다.
공정능력 지수에는
전통지수인 Cp, Cpk, Pp, Ppk와 6시그마인 DPU, DPMO, Zst, Zlt, Zbench등이 있습니다.
데이터의 유형에 따라 공정능력을 다르게 측정하게 됩니다.

공정능력 지수에 추가적으로 알아보자면,
Z는 표준 정규분포표에서의 z변수를 말합니다.
Zbench값은 그 값까지의 확률이 공정 능력으로 여겨지고,
Zst는 단기 공정능력, Zlt는 장기 공정 능력을 말합니다. (Zlt = Zst + 1.5, 보통 Zlt=4.5면 6시그마 만족)
FTY는 first time yield로, 처음 공정을 진행했을 때 수율을 말하고,
DPU는 특정 단위 결함 갯수, DPMO는 100만개 중 결함 갯수를 말합니다.
- 공정능력 지수
다양한 공정능력 지수 중 Cp, Cpk, Cpm, Pp, Pp,에 대해 알아봅시다!
1. Cp, Cpk
(1) Cp
Cp를 쉽게 이해하자면 농구공과 농구 골대의 예시를 들 수 있습니다.
기존 농구공과 농구골대를 가지는 상황을 Cp=1이라 하고,
농구공이 반으로 줄거나, 골대가 2배가 된다면 Cp=2가 되게 됩니다. 즉 양품 생산 확률이 증가한다는 것이죠.
정리하자면 치우침이 없는 경우의 잠재적 공정능력을 Cp라고 합니다.
오로지 공정산포에 의해서만 결정되기 때문에, 공정결과의 치우침을 반영하지 못합니다.
규격이 한쪽만 존재한다면, 치우침을 반영하지 않아도 됩니다.
Cp값과, Cpu(USL에 대한 Cp), Cpl(LSL에 대한 Cp)는 다음과 같이 구할 수 있습니다.
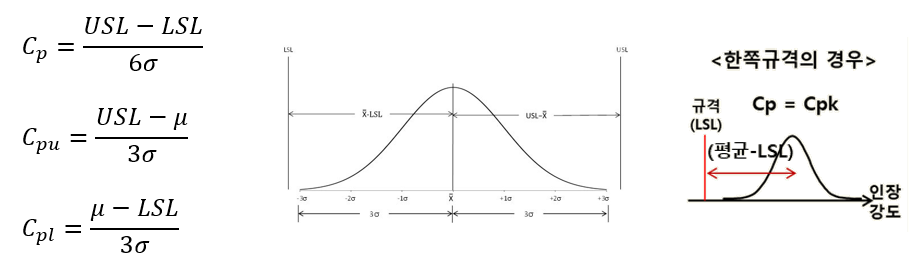
(2) Cpk
양쪽구격이 존재할 경우, 치우침과 산포를 같이 고려해 공정능력을 평가하는 Cpk를 사용합니다.
어느 한쪽 규격이라도 넘어가면 안되기 때문에 평균과 가까이 있는 규격을 기준으로 공정능력을 평가하게 됩니다.
즉, Cpu와 Cpl의 최소값을 취해 치우침을 반영할 수 있게 됩니다.
한쪽 규격만 존재하면 Cp=Cpk가 성립하게 됩니다.

Cp와 Cpk를 비교하면 아래와 같습니다.
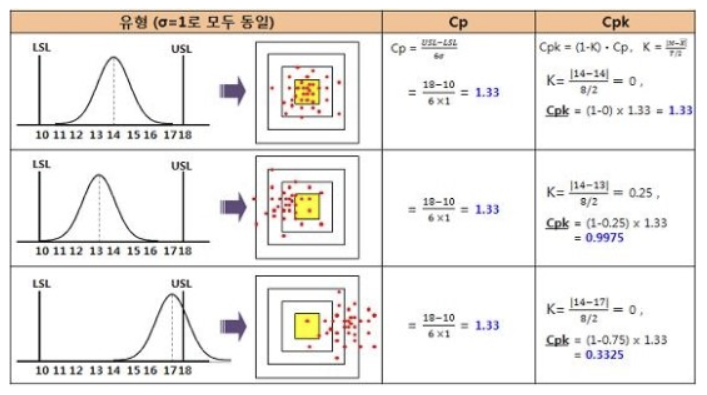
중심이 치우쳐 있어도 Cp에는 반영이 되지 않습니다. 즉, Cp값이 좋다고 공정능력이 좋다고 말할 수 없다는 것이죠.
(3) Cp, Cpk 판정
공정능력지수가 1.67이상이면 공정능력이 충분하다고 판단할 수 있습니다.
평균이 target에 벗어난 경우에는 Cpk로 대체하여 공정능력을 판단할 수 있게 됩니다.
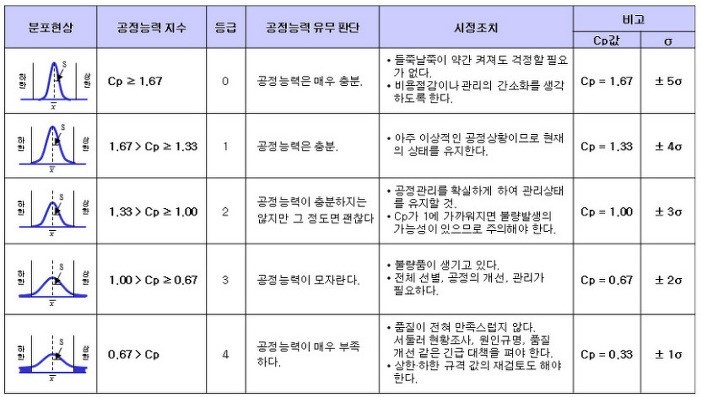
가장 이상적인 상황은 '공정능력 충분' 상황으로, 회사에서는 이 상황을 유지하고, 생산성 향상을 고려해볼 수 있습니다.
반면, 공정능력 부족 상황과 매우 부족 상황은 설비를 버리고 공정이 불가능한 상황으로 판단해야 합니다.
추가적으로, Cpk=2인 상황은 6시그마를 달성했다고 할 수 있습니다.
2. Cpm
Cpm은 장비산포지수입니다.
평균이 target을 벗어나도 편차를 줄이면 공정 능력이 유지되며 왜곡이 생길 수 있습니다.
다시말해 평행이동 된 그래프에서 산포가 증가해 폭이 좁아진다면 Cpk가 동일하게 될 수 있다는 것이고, 기존의 공정능력 대비 좋다고 말할 수 없을겁니다.
그래서 Cpm을 이용해 target 대비 centering 수치를 보강하는 것이 바로 장비산포지수 입니다.
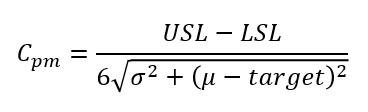
(μ-target)값을 통해 공정능력수치에 target과 평균간의 차이를 수치에 반영시키는 것 입니다.
3. Pp, Ppk
Pp와 Ppk는 장기적인 개념의 산포지수입니다.
Cp와 Cpk의 경우 단기적인 공정능력을 평가하기 때문에, 수치의 군내변동만을 고려하게 됩니다.
반면 Pp와 Ppk는 장기적인 공정능력을 평가하고자 군내변동+군간변동을 모두 고려합니다.
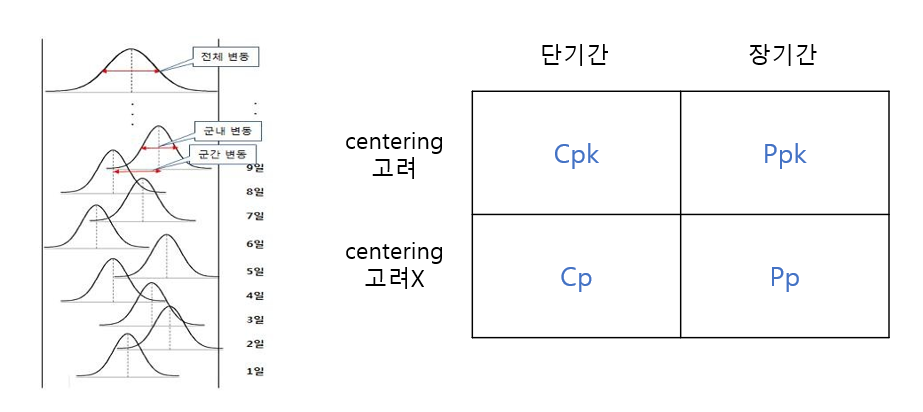
일반적으로 Pp, Ppk가 Cp, Cpk보다 작은 값을 가지고 있습니다.
엑셀 실습을 해보겠습니다!
1) Cp, Cpk
2) Pp, Ppk
위에 사용한 수식들(Cp, Cpk, Pp, Ppk) 을 엑셀 함수로 적용시켜서 구하면 됩니다!
(average 함수, min함수, sigma도출을 위한 stdev.p함수)
오늘 글은 여기까지!
감사합니다 :)

'[학부 일기] 그 외 활동 > 데이터 분석' 카테고리의 다른 글
| [반도체데이터분석] 상관분석 (0) | 2023.08.24 |
|---|---|
| [반도체데이터분석] 가설검정 (0) | 2023.08.21 |
| [반도체데이터분석] Data 유형 (0) | 2023.08.18 |
| [반도체데이터분석] Data 분석의 기초 (1) | 2023.08.16 |
| [반도체데이터분석] 데이터 분석 (2) | 2023.08.16 |