안녕하세요!
이번 데이터분석에서 다룰 내용은 '분산분석'입니다.
데이터 분석의 꽃...!! 저는 배우면서 너무 재밌었어요 ㅎㅎ
배운대로 잘 정리해보겠습니다!
< 분산 분석 >
- 분산분석(Analysis of Variance => ANOVA)
분산분석은 2개 이상 하위모집단 간의 평균 차이가 통계적으로 유의한지 검증하는 과정을 말합니다.
귀무가설 H0은 모든 평균에 차이가 없다를 가정하고, 대립가설 H1은 평균에 차이가 있다를 가정합니다.
하위모집단 간의 분산(특정 요인에 의한 변동)과 하위모집단 내의 분산(우연에 의한 변동)을 비교하는데,
이때 사용하는 분석은 F분석을 사용해 유의수준에 비교하여 검증하게 됩니다.
평균차이가 많이나고 각각 분산이 적당한 경우 그에따른 요인이 실험에 영향을 미치는구나라고 판단할 수 있습니다.
- 분산분석 수식
분산분석에 사용되는 수식은 아래 3개가 있습니다.
(1) SSW (Sum of Squares Within Groups)
하위 모집단 내 변동으로, 각 하위모집단으로 부터 추출된 표본의 평균과 각 표본 데이터 차이의 제곱 합을 말합니다.
(편차제곱의 합)
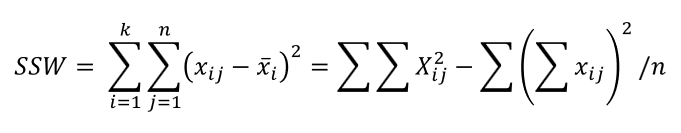
(2) SSB (Sum of Squares Between Groups)
하위 모집단 간 변동으로, 각 하위모집단의 표본평균과 전체 표본평균과의 차이의 제곱 합을 말합니다.
(그룹평균과 전체평균과의 차이)

(3) SST (Sum of Squares Total)
총 변동으로, 하위모집단 간/내 변동의 총 합을 말하게 됩니다.

대충, SSB가 SSW보다 커야 유의미한 차이를 보이겠다고 분석할 수 있습니다!
- 분산분석표 - ANOVA table
분산분석에 사용하는 분산분석표, ANOVA table에 대해 알아보겠습니다.
가설검정을 위해 변동을 중심으로 여러 계산과정을 사용하기 때문에, 이를 간단히 알아보기 위해 종합한 표입니다.
변동의 분해를 통해 결과를 분산분석표로 단순하게 정리할 수 있습니다.

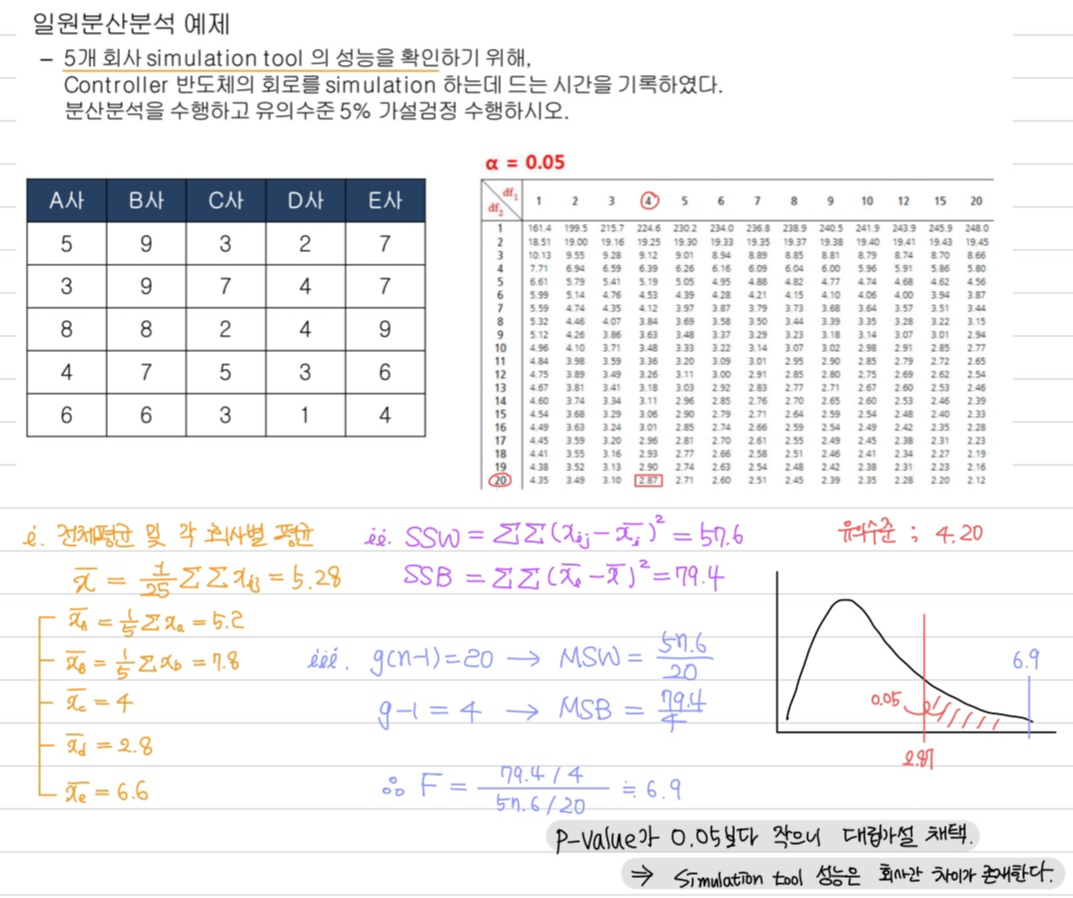
- 일원분산분석 (one-way ANOVA)
일원분산분석은 하나의 특정요인에 의해 2개이상의 하위모집단으로 구분되는 경우에 사용합니다.
독립변인이 1개, 종속변인이 1개인 상태로, 2개이상의 하위모집단 평균이 동일한지 검정합니다.
즉, 특정 요인이 모집단의 평균에 영향을 미치는 변수인지 확인하게 됩니다.
하위모집단 수는 2개 이상으로 제한없이 사용하게 됩니다.
일원분산분석에는 관찰의 독립성(하위모집단에서 표본은 독립적으로 표집)
정규성(하위모집단 변수는 정규분포 따름)
등분산성(하위모집단 내 분산 동일) 이라는 세가지 가정을 가지고 진행하게 됩니다.
아래 예시를 통해 일원분산분석을 이해해보면 좋을 것 같네요:)
- 이원분산분석 (two-way ANOVA)
이원분산분석은 2개의 특정요인에 의해 다수의 하위모집단으로 구분되는 경우에 사용합니다.
하위모집단의 평균이 동일한지 검정하여, 특정 요인이 모집단 평균에 영향을 미치는 변수인지 확인하게 됩니다.
교호작용이 존재할 수 있기 때문에 이를 고려하여 진행해야 합니다.
이때에도
귀무가설 H0은 하위모집단의 평균은 차이가 없다이고,
대립가설 H1은 하위모집단의 평균에 차이가 있다로 진행하게 됩니다.
이원분산분석의 데이터의 형태는 아래와 같습니다.

요인 A의 i번째 수준과 요인 B의 j번째 수준에서 측정된 k번째 관측값을 Y_ijk라 하게 됩니다.
이원분산분석이기 때문에, 총 4개의 편차가 존재합니다 -> A요인, B요인, 교호작용, 오차

교호작용이 있으면 교호작용 편차에 >0의 값이 나오고, 교호작용이 없으면 0의 값이 도출됩니다.
SSA, SSB가 SSE에 비해 크면 A와 B는 영향이 있다라고 판단하게 됩니다.
그리고 이들을 통해 two-way ANOVA table을 작성하면 아래와 같이 작성할 수 있습니다.

이원분산분석의 검정은 일원분산분석보다 복잡합니다.
ⅰ) 교호작용 확인
귀무가설 H0은 모든 실험결과는 동일하다 (교호작용이 없다)를 사용합니다.
검정통계량은 MSAB/MSE를 통해 p-vale를 평가하여 유의수준보다 작으면 교호작용이 있는 것으로 판단합니다.
ⅱ) A의 주효과 확인
귀무가설 H0은 모든 실험결과는 동일하다 (A로 인한 영향이 없다)를 사용합니다.
검정통계량은 MSA/MSE를 통해 p-vale를 평가하여 유의수준보다 작으면 A로 인한 영향이 있는 것으로 판단합니다.
ⅲ) B의 주효과 확인
귀무가설 H0은 모든 실험결과는 동일하다 (B로 인한 영향이 없다)를 사용합니다.
검정통계량은 MSB/MSE를 통해 p-vale를 평가하여 유의수준보다 작으면 B로 인한 영향이 있는 것으로 판단합니다.
엑셀로 실습을 해봅시다!
먼저 데이터분석 툴로 분산분석을 진행할 수 있습니다.
데이터 분석 > 분산 분석 : 일원 배치법 -> 원하는 데이터 값 구간만을 선택하면 됩니다.
데이터 분석 > 분산 분석 : 반복이 있는 이원배치법 -> 항목까지 포함해 데이터 범위를 설정해야 합니다.
원하는 요인에 따라 각각 평균을 구하고,
SSW는 요인의 VAR.P()*요인갯수 를 모두 더해서 구할 수 있습니다.
SSB는 구해둔 평균들의 VAR.P()를 구해 이 값에 요인갯수와 하위모집단 갯수를 곱해줍니다.
(VAR.P()*요인갯수*하위모집단갯수)
둘을 각각 자유도로 나누어 MSB와 MSW를 구한 후 나오는 F-value값과 유의수준(F.INV(0.95, 자유도, 자유도))를 비교해
영향을 확인할 수 있습니다.
이원배치법에서는 더 복잡하게 값을 구해야 합니다.
위에 진행한 것들을 반복하여 SSA와 SSB를 구할 수 있는데,
SSAB같은 경우에는 알고있는 수식 (데이터-a평균-b평균+ab평균)^2을 통해 구하고 모두 합한 뒤, 시행횟수로 곱해주기 까지 해야합니다..ㅎㅎ
SSE는 각각 VAR.()를 구하고 모두 더한 다음 시행횟수로 곱해주면 됩니다.
이 값들을 통해 MSA, MSB, MSAB, MSE를 구하고 F-value와 유의수준을 비교하면 됩니다!
오늘 글은 여기까지입니다!
데이터 분석 게시글.. 다음이 마지막입니다.. 생각보다 빨리 진행되네요
다음 요인배치법까지 열심히 써보겠습니다!!

감사합니다 :)
'[학부 일기] 그 외 활동 > 데이터 분석' 카테고리의 다른 글
| [데이터분석] 윈스펙 K디지털기초역량훈련 후기 (2) | 2023.09.14 |
|---|---|
| [반도체데이터분석] 요인배치법 (0) | 2023.08.31 |
| [반도체데이터분석] 실험계획법 (0) | 2023.08.28 |
| [반도체데이터분석] 관리도 (0) | 2023.08.28 |
| [반도체데이터분석] 회귀분석 (0) | 2023.08.25 |