안녕하세요 :)
데이터분석 마지막 글, 요인배치법에 대해 알아보려 합니다!
앞에서는 실험을 설계하고, 유의미한 결과들의 관계를 확인했다면,
이번 글에서는 각 요인을 구체적으로 define하고 실험 스킬을 효율적으로 하는 요인배치법에 대해 알아보겠습니다!
마지막까지 파이팅해서 써보겠습니다!
<요인배치법>
- 요인배치법(Factorial Design)
요인 실험은

과 같이 나타내고, 모든 인자간의 수준 조합에서 실험을 진행하게 됩니다.
반복을 피해도 최소한 K^n번 실험을 해야하고, 랜덤한 순서로 진행해야 합니다.
요인실험은 모든 요인들의 주효과(인자 단일효과)와 2인자간의 교호작용을 추정할 수 있습니다.
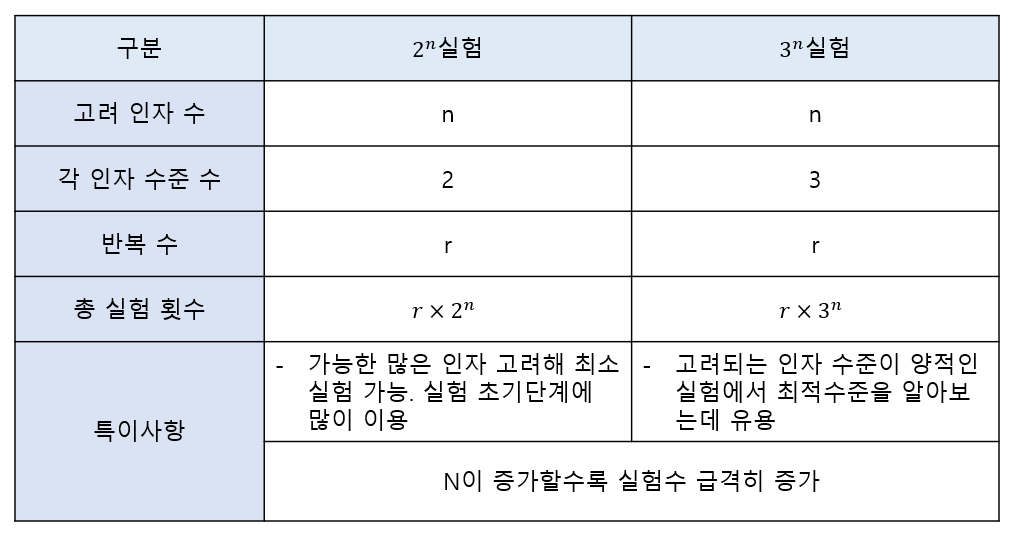
고려되는 인자 수에는 제한이 없지만, 2^n 부분배치법은 2^n번 실행하게 됩니다.
실험 계획 초기에 인자가 많다면 screening 기법을 통해 핵심인자를 찾아낼 수 있습니다.
screening기법은 각 인자의 변화가 큰 인자를 최적치로 사용하는 기법입니다.
- 요인배치 설계의 종류
요인배치 설계는 완전요인 배치법, 부분요인 배치법 두개로 구분됩니다.
둘 다 실험의 초기단계에서 중요한 인자를 식별하는데 사용되는 방법입니다!
(1) 완전요인 배치법 (Full factorial Desing)
각 인자별 수준수가 다를 경우, 모든 인자의 수준 조합에서 실험하도록 설계하는 방법입니다.
모든 인자의 효과와 교호작용을 추정할 수 있지만,
인자수와 수준수가 많아지면 실험 횟수가 기하급수적으로 증가하기 때문에 실제 사용에 제약이 있습니다.
(2) 부분요인 배치법 (Fractional Factorial Design)
완전요인설계의 1/2, 1/4 정도만 실험을 실시하는 방법입니다.
현실적으로 의미가 적은 고차의 교호작용을 희생하고, 중요한 주효과와 2차 교호작용만 추출할 수 있게 실험횟수를 줄이게 됩니다.
예를들어, 반도체 공정에서 실험을할 때, 실외 온도나 미세먼지 수치는 인자에 고려하지 않아도 될 것입니다.
특히, 2수준(2^k) 요인 배치는 모든 인자 수준이 2인 상황에서 사용하게 됩니다.
이는 단순하고 효율적이기 때문에, 산업계에서 가장 일반적으로 사용되는 실험계획입니다.
2수준과 3수준을 비교하면 아래 표와 같이 비교할 수 있을겁니다!
- 실험 Data 형태
2수준 요인실험에서 k가 2, 3, 4일 때를 비교해 봅시다!
- 2² 요인 실험

- 2³ 요인 실험
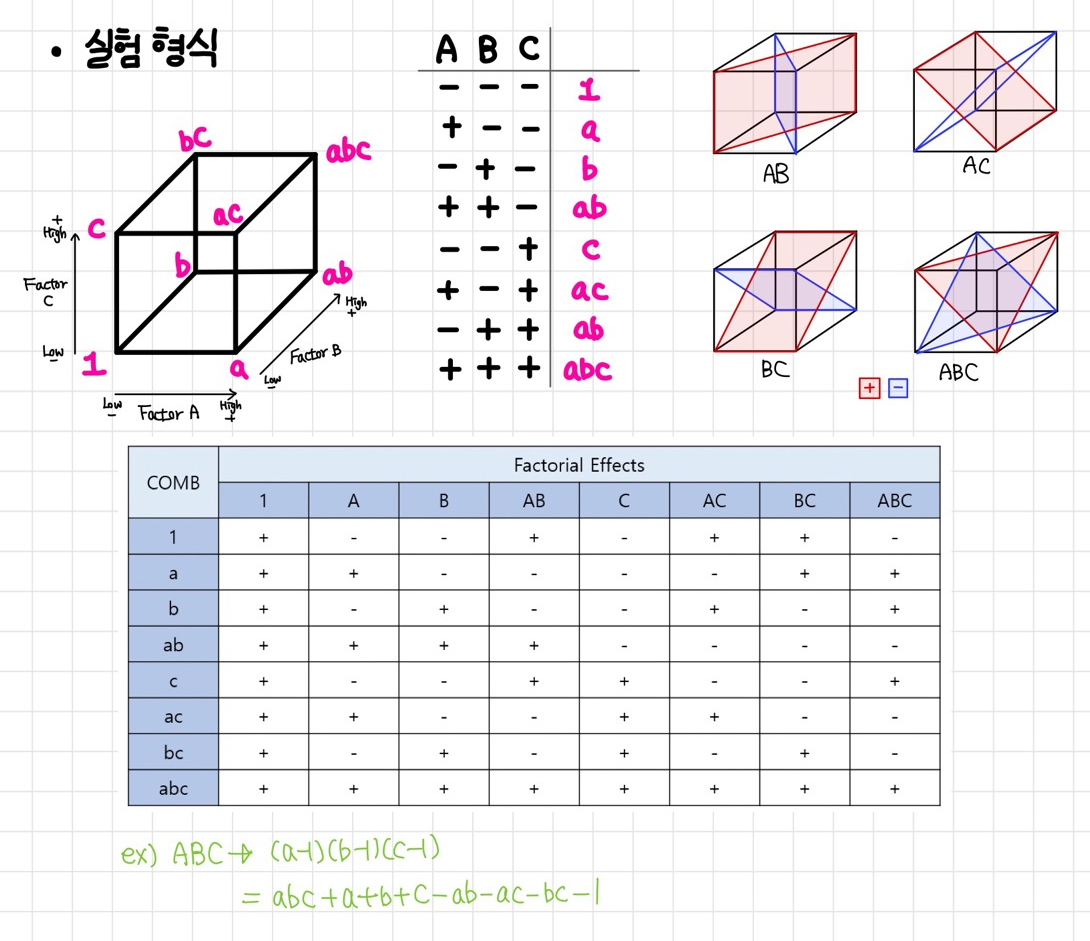
- 2⁴ 요인 실험

추가로, 주 효과와 교호작용이 효과보는 인자를 찾는 쉬운 방법은
인수분해식을 이용하면 쉽게 사용할 수 있습니다.
예를들어 ABCD 4개 인자에서,
ABCD 교호작용은 (a-1)(b-1)(c-1)(d-1)에서 양수값을 가지는 인자는 영향을 받는 인자가 됩니다.
AD의 교호작용은 (a-1)(b+1)(c+1)(d-1)에서 양수값 인자를 찾으면 됩니다.
- 교호작용
교호작용은 2개 인자 이상 특정한 인자 수준의 조합에 의해 일어나는 효과를 말합니다.
3개 이상의 인자 조합 효과를 고차의 교호작용이라 하고, 주요인자 외 인자 조합은 case가 많아지기 때문에 보통 잘 구하지 않는다고 합니다.
일반적으로 2개의 교호작용을 구하고, 가끔 3개 인자도 고려한다고 합니다.
교호작용의 유무는 한 인자의 효과가 다른 수준의 변화에 따라 변할 때 존재한다고 합니다.
예를들어, 반도체 wafer 수율에 미치는 gas 농도의 효과가 온도 수준에 따라 다르고, 아래 표를 따른다면

위와 같이 두 그래프는 평행하지 않기 때문에 교호작용이 있다고 판단합니다.
하지만, 교란변수를 유의해야 합니다.
상관관계가 있지만 실제 인과관계에 있지 않은 변수를 교란변수라 하기에, 이를 잘 걸러내고 인자를 선별해야 합니다.
또한 앞 실험계획법에서 배운 반복, 블록, 랜덤화의 원리도 적용해야합니다.
특히, 블록의 원리를 적용할 때는, 각 블록 내 실험 환경은 동일하게 맞춰주어야 합니다.
- Pooling
pooling은 통계적으로 유의하지 않은 항을 오차항에 넣어 새로운 오차항으로 만드는 것 입니다.
교호작용의 오차항 기준은
- 최고차 항을 우선적으로
- 실험 목적을 고려해 기술적으로 의미없는 교호작용
- 교호작용 효과가 작은것 우선적으로
합니다.
되도록이면 주효과는 pooling하지 않야아 합니다.
- 부분요인 배치법
부분요인배치법은 인자수가 증가할 때, 실험횟수가 exponential로 증가하는것을 막기 위해,
일부를 희생시켜 실험 전체 크기를 작게 하는 방법입니다.
(반면 교락법은 실험 전체 크기를 줄이는 것이 아닌 블록의 원리를 적용해 동일환경 내 실험을 조절하는 것입니다.)
불필요한 교호작용이나 고차의 교호작용을 구하지 않고, 인자의 조함 중 일부만을 실험하게 됩니다.
보통 screening단계에서 여러 인수들 중 일부를 선별할 때 사용합니다. (초반에)
1/2 부분 요인 실험은 2³진행할 요인실험을 4번 실험으로 효과를 분석하는 방법입니다.
최고차 교호작용 ABC를 교락시켜 한 개 블록만 실험하게 됩니다.

위를 증명해보면,
- 블록 1 조합 실험 시

- 블록 2 조합 실험 시

와 같이 교호작용까지 근사하여 구할 수 있게 되고 실험 횟수를 줄일 수 있습니다.
물론 실제 측정치와 오차는 당연히 존재합니다!
- 교락법
이러한 교락법은 동일 환경 내 실험 횟수를 줄여 주효과와 블록효과는 교락되지 않습니다.
고차의 교호작용을 불록에 교락시켜 실험의 정도를 향상시킬 수 있습니다.
예를들어, 16번 실험을 8번씩 이틀에 거쳐 수행한다면, 1일은 1블록, 2일은 2블록을 진행하게 됩니다.
ABC의 교호작용은 Block 효과의 차이로 구할 수 있고, 이외의 모든 효과는 차이에 관계없이 구할 수 있습니다.
엑셀 실습을 진행해 봅시닷!
완전요인 실험은 간단하게,
반복으로 인한 값들을 평균낸 뒤, A에 의한 효과 (ab+a-b-1)/2 와 B에 의한 효과 (ab+b-a-1)/2
그리고 AB 교호작용 (ab+1-a-b)/2를 이용해 최적조건을 찾을 수 있습니다.
물론 요인이 3개면 SUM함수를 써서 각 주효과와 교호작용을 파악해낼 수 있습니다!
각 요인에 대한 효과와 교호작용을 파악하고, abcd값을 error로 파악하여 오차항을 계산할 수 있습니다.
이 오차항보다 제곱값이 작은 효과들은 오차에 pooling하여 최종 오차항을 구한 뒤,
각 제곱값에 오차항을 나누어 F-value를 구할 수 있습니다.
유의수준은 F.INV(0.95, 1, 오차항자유도)를 통해 구하여 유의한 인자를 구해낼 수 있습니다!
여기까지 데이터분석 강의가 끝이 났습니다..!
약 3주동안 들으면서 정말 재밌었어요.. 식스시그마 공부할 때도 생각나고..
데이터 분석 기법들을 엑셀로 직접 진행한다는 점이 흥미로웠던 것 같네요 ㅎㅎ
아마 다음 마지막글은, 블로그 후기글로 마무리할 것 같아요!
읽어주셔서 감사합니다!

안녕!
'[학부 일기] 그 외 활동 > 데이터 분석' 카테고리의 다른 글
| [데이터분석] 윈스펙 K디지털기초역량훈련 후기 (2) | 2023.09.14 |
|---|---|
| [반도체데이터분석] 분산분석 (0) | 2023.08.29 |
| [반도체데이터분석] 실험계획법 (0) | 2023.08.28 |
| [반도체데이터분석] 관리도 (0) | 2023.08.28 |
| [반도체데이터분석] 회귀분석 (0) | 2023.08.25 |