안녕하세요 바니입니다 :)
오늘은 P-N Junction의 개념과 평형상태에서의 다양한 요소들에 대해 정리해 보려 합니다.
- P-N Junction
우선 P-N Junction은 n-type 반도체와 p-type 반도체 사이의 junction을 말합니다. 이를 이용해서 Diode, Solar cells, transistor들이 만들어 집니다. 아래 그림은 P-N Junction의 구조를 나타낸 그림입니다.

p-type의 방면에서 P-N Junction을 살펴보자면, p-type에 있는 acceptor의 hole, h+가 n-type으로 diffusion하게 되면서, p-type의 side에는 (-) space charge를 띄게되고, 전체적으로는 중성을 띄게 됩니다.
반대로 n-type은 donor가 존재하고, donor의 electron인 e-가 diffusion되면서 n-type의 side에는 (+) space charge를 띄고, 전체적으로 중성을 띄게 됩니다.
이러한 P-N Junction에는 diffusion이 멈추고 평형상태가 되면 space charge가 생기게 되고, 전기장이 형성됩니다. junction의 외부에는 전기장이 형성되지 않습니다. 그리고 이러한 space charge가 있는 영역을
space charge region = depletion region = transition region => W
라고 부릅니다.
Energy band에서 Vo는 n-type 반도체와 p-type이 가지는 전위차의 높이를 말합니다. 이 전위차는 depletion region에만 형성되는데, junction의 외부에 전기장이 형성되지 않기 때문입니다.
위 그림에서 P-N Junction의 particle flow와 current를 알 수 있습니다. 각각의 흐름은 쉽게 알 수 있을 것 입니다ㅎㅎ
junction의 외부에는 전기장이 없기에 net current는 junction을 가로질러 흐를 수 없고, 이는 다음과 같이 정의됩니다.

- Built-in potential
Built-in potential은 Vo (V_o)로 나타내고, depletion region의 전기장에 의해 걸리는 전압, contact potential을 말합니다. 이를 구하기 위해서는 net current는 depletion region인 (W)에만 흐른다고 가정해야 합니다. 즉 위의 정의를 이용해 풀 수 있습니다. 이 Built-in potential을 구하는 방법은 2가지가 있습니다.
① 위의 정의를 직접적으로 사용하는 방법
우선 p-type에서 hole을 기준으로 구해보겠습니다. n-type의 electron을 기준으로 구하셔도 같은 결과가 도출됩니다!

위 식에서 J는 물리전자1에서 배우는 Current density 입니다. 이 식에 E(x)와 V(x)의 관계식과, Einstein relation을 적용하여 전개하면,
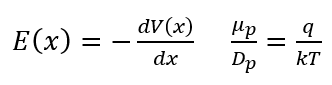

위와 같은 식이 주어집니다. 위 식의 V(X)를 Vn ~ Vp까지 적분 (p(x)를 p_n~p_p)하면 다음과 같습니다.

우리가 알고자 했던 Vo은 Vn - Vp가 됩니다(위의 Energy bands그림 참조). 그렇기에 Vo에 대해 정리를 하면,

와 같이 Bulit-in potential을 구할 수 있습니다.
② Energy bandgap을 사용하는 방법
위와 달리 band gap을 사용해 구하는 방법도 존재합니다.

우리는 Vo가 p-type의 intrinsic level과n-tupe의 intrinsic level의 차이라는 것을 알 수 있습니다. 이를 물리전자1에서 배웠던 electron과 hole의 농도를 통해 Built in potential을 구해보면 다음과 같이 구할 수 있습니다.

- 평형상태에서의 Fermi level
P-N Junction의 평형상태, equilibrium상태에서의 Fermi level은 constant합니다. 일정하다는 것 입니다. 이 또한 식으로 증명해 볼 수 있습니다. 위에서 사용했던 식을 이용해 구해보면,

위와 같이 n-type과 p-type의 Fermi level이 같음을 알 수 있고, 즉 평형상태에서는 일정함을 알 수 있습니다!
- Junction의 space charge
다음은 Junction의 space charge에 대해 알아보겠습니다. transition region 내부에서 electron과 hole들은 서로 다른 방향으로 넘어가고 싶어 하는 경향을 보입니다. electron들은 diffusion으로 인해 n-type에서 p-type으로 이동하지만 내부의 E-field로 인해 몇몇은 p-type에서 n-type으로 drift됩니다. 반대로 hole들 또한 적용됩니다. 이렇게 W 내부의 carrier들이 depletion되고 외부는 E-field 없이 중립상태를 유지하는 상태를 Depletion approximation이라 합니다. 아래의 그림들과 표는 P-N Junction의 depletion영역에서의 Charge density와 E-field를 나타낸 그림과 그래프 입니다.

Charge density 그래프에서 면적은 Charge의 양이 되고, x= 0인 지점은 charge가 max인 지점이 됩니다. x_no는 n-type쪽으로 depletion된 부분이고, x_po는 p-type쪽으로 depletion된 부분입니다. n-type부분의 W에 있는 Charge의 양과 p-type부분의 W에 있는 Charge의 총 합, 즉 두 사각형의 면적은 같음을 이용하여 다음과 같이 식을 유도할 수 있습니다.

또 E(x)와 charge의 관계식을 이용하면 E-filed에서 나타나는 기울기 또한 알 수 있습니다.

가우스의 법칙을 통해 E-filed와 carrier들의 농도에 관한 식을 이용해 PN juncion에서 x=0일 때의 전기장, Eo를 다음과 같이 구할 수 있습니다.

- depletion width, x_no, x_po
위 식들에 위에서 구했던 Vo와, charge density에서 보았던 식들을 이용하여 W, x_po, x_no를 구해봅시다. 먼저
Eo를 구해보았으니, E(x)를 구하기 위해 charge density에서 구했던 식과 W를 x에 대해 나타낸 식을 사용하면,


위와같이 전기장을 구할 수 있습니다.

위 식들에 built in potential을 대입하면 W를 구할 수 있고, 각각의 x로 분해하면 x_no와 x_po를 쉽게 구할 수 있습니다.
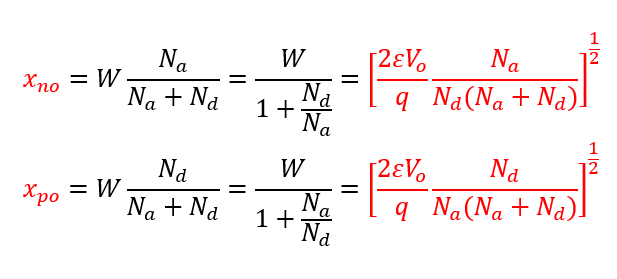
오늘 정리한 PN juncion에서 핵심요소는 x_po, x_no, W가 어떠한 요소로 구성되어 있는지, 그리고 E_o는 어떻게 구할 수 있는지가 포인트인 것 같습니다. 수식이 많지만 각각의 원리를 이해하면 쉽게 이해하고 외울 수 있을겁니다ㅎㅅㅎ
다음 포스팅에서는 이러한 PN juncion에 외부 전압을 걸어주었을 때 어떠한 현상이 일어나는지에 대해 알아보도록 하겠습니다! 감사합니다♡

'[학부 일기] 전자공학과 전공 > 물리전자II' 카테고리의 다른 글
| [ 물리전자II ] Metal-Semiconductor Junction (0) | 2022.02.15 |
|---|---|
| [ 물리전자II ] P-N Junction의 Forward bias와 Reverse bias (3) (0) | 2022.02.15 |
| [ 물리전자II ] P-N Junction의 Forward bias와 Reverse bias (2) (0) | 2022.01.04 |
| [ 물리전자II ] P-N Junction의 Forward bias와 Reverse bias (1) (0) | 2022.01.03 |
| [ 물리전자II ] Fabrication Process : 공정 과정 (0) | 2021.10.30 |